扩展欧几里得算法的 Python 程序
pythonserver side programmingprogramming更新于 2024/1/23 1:15:00
在本文中,我们将了解下面给出的问题陈述的解决方案。
问题陈述 − 给定两个数字,我们需要计算这两个数字的 gcd 并显示它们。
GCD 两个数字的最大公约数是可以整除它们两个的最大数字。在这里,我们遵循欧几里得方法来计算 gcd,即反复除以数字并在余数变为零时停止。在这里,我们根据递归中获得的先前值扩展算法。
现在让我们观察下面实现中的解决方案 −
示例
# 扩展欧几里得算法
def gcdExtended(a, b, x, y):
# 基本情况
如果 a == 0 :
x = 0
y = 1
返回 b
x1 = 1
y1 = 1 # 存储结果
gcd = gcdExtended(b%a, a, x1, y1)
# 使用之前计算的值更新 x 和 y
x = y1 - (b/a) * x1
y = x1
return gcd
x = 1
y = 1
a = 11
b = 15
g = gcdExtended(a, b, x, y)
print("gcd of ", a , "&" , b, " is = ", g)
输出
gcd of 11 & 15 is = 1
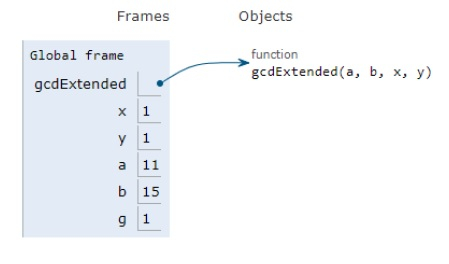
所有变量均在局部范围内声明,其引用如上图所示。
结论
在本文中,我们了解了如何为扩展欧几里得算法编写 Python 程序

